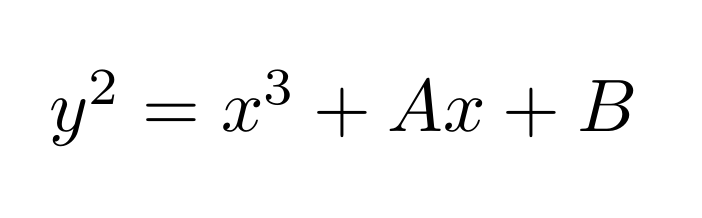Trusted Setup with Isogeny-based Cryptography

Trusted parties are fundamental in seting up secure communication among parties. For instance, a trusted setup is needed when establishing a trusted relationship between users and certain public information in a public-key infrastructure (PKI) for public-key encryption and signature schemes.

The risk with placing trust on a third party can be seen when they misbehave, causing the security of the scheme to be compromised. For example, if the trusted certificate authority of a PKI is corrupted and issues certificates for users without verifying their identities, there is no longer a guarantee on the privacy and authenticity of the communication.

For the full blogpost, click here.

-M x

New Blog Features!

I’m happy to announce that I have two new features on my new blog:

  • You can now subscribe! Use the link either in the header or at the bottom of each post. Once you subscribe, you will be updated by email when a new post is up.
  • You can share on Facebook, Twitter etc. using the red button on the bottom right of each post. Currently, this doesn’t work on Firefox, but it does work on Chrome!

The next step is getting a comment box at the end of each post! M x

MOVED BLOG

Just a quick post to let you all know that have decided to shift my blog onto GitHub: mariascrs.github.io. This way I can integrate Latex easily into my posts! I still haven’t figured out how to get a subscribe feature on the website but don’t worry, I will continue to post links to my new blog posts on this blog so you can still be notified when I post!

I have just posted a new post on ‘Isogenies for Cryptography’ so let me know what you think. – M

Post Quantum Cryptography – The Basics

Post-quantum cryptography aims to find schemes that can withstand an attack from a quantum computer. This is becoming an increasingly important field of research as the development of quantum computers intensifies and current cryptography schemes relying on the difficulty of factorisation can be broken in polynomial time by these quantum computers. So, researchers have tried to find other ‘hard’ problems in mathematics (take exponential time to solve) that can be exploited to create classical crypto schemes that withstand attack of quantum computers (at least for now).

In general post-quantum schemes require more resources compared to traditional cryptography, in particular Elliptic Curve cryptography; security against quantum computer attacks come at a cost. There are four different families of post-quantum schemes that are considered to be the best candidates, and in this blog post I will briefly discuss each of them.

Code-Based Cryptography

Traditionally, error-correction codes are used to detect and correct bit errors when messages are transmitted over an unreliable channel. The code can be chosen to fulfil the requirements of the channel; in particular the number t of correctable bit errors can be determined.

Decoding arbitrary codes is computationally hard and can be infeasible depending on the code parameters. However, there are specific codes for which efficient decoding algorithms are known. So in practice only such codes are used that have efficient decoding algorithms.

The main security assumption of code-based cryptography is the difficulty of decoding a random linear code. Even with quantum computers, only exponential-time algorithms are known.

The first code-based public key crypto system was proposed by McEliece in 1978 and has not been fundamentally broken since, however the main problem with this is the size of the keys: it requires key sizes of about 4MB in order to achieve post-quantum security. Niederreiter introduced a scheme that gave some improvements to the encryption and decryption cost and required smaller keys.

There have been many attempts to reduce key sizes by using different codes that have some redundant structure in the public key. But this structure has led to efficient classical attacks on the crypto-systems. 

There are also signature schemes, hash functions and random number generators based on code-based cryptography. 

Lattice-Based Cryptography

The underlying ‘hard’ problem is the shortest vector problem (SVP): a basis of a vector space V and a norm N are given for a lattice L and one must find the shortest non-zero vector in V, as measured by N, in L. It is believed that the SVP is computationally hard even for quantum computers.

NTRUEncrypt is a commercial public key encryption scheme based on lattices. Public key sizes of about 1.5kB to 2kB are required in order to achieve the desired security. Note that these are the requirements based on the algorithms that have (up to today) been developed to solve the SVP. These restrictions are called ‘parameters’.

Closely related is the signature scheme NTRUSign. However, the security of this is not yet well understood and so there are no recommendations for these signature schemes for post-quantum security.

There are also key exchange protocols that are built on lattice-based cryptography, such as NewHope that has been experimentally adopted by Google. NewHope is not symmetric and needs two rounds of agreement (unlike the Diffie-Hellman Key Exchange). Also, it does not include authentication, so this needs to be achieved by other means.

By switching to post-quantum key exchange now, an attacker in the future does not learn encryption kets even if he breaks long-term authentication keys. Therefore, combining a post-quantum key exchange with a classical authentication scheme provides a cost effective long-term secure authenticated key exchange for the interim period until all cryptographic primitives have been transitioned to post-quantum secure schemes.

Hash-based Cryptography

Hash functions are one-way functions tha tmap bit strings of an arbitrary length to relatively short, fixed length bit strings called hash values. There are three required properties:

  • Pre-image resistance: must be hard to compute a pre-image of a hash value i.e. a bit string that once hashed results in a given hash value.
  • Second pre-image resistance: given a bit string, it must be hard to find a different bit string that has the same hash value.
  • Collision resistance: it must be hard to find two arbitrary bit strings that have the same hash value.

Since by definition it is not computationally feasible to compute the inverse of a hash function it is not known how to construct public-key encryption schemes using hash functions. However, it is possible to construct signature schemes, where in general the required signature size increases if more signatures for the same public key are needed.

Hash-based signature schemes have been around for a long time and so the estimates of the required parameters to achieve post-quantum security are very reliable.

Multivariate Cryptography

This is based on the difficulty of the MQ-problem: solving multivariate quadratic systems of equations over finite fields is NP hard (no efficient algorithm for solving random multivariate polynomial systems). The difficulty depends on the size of the underlying field, the number of variables and the degree of the system. If the number of equations and variables is sufficiently large then even quadratic equations over a the field with two elements are hard to solve.

For constructing an asymmetric public-key scheme, the public-key itself is a set of multivariate quadratic polynomial and the private key often is the knowledge of a trapdoor that allows to efficiently solve the multivariate system. The construction of the scheme allows the use of systems with more variables than equations, so there may be more that one solution. Any of these solutions is a valid signature.

The confidence in multivariate systems is quite high however a relatively large public key is required. Attempts to reduce key sizes by using few variables over larger fields, but the security of such systems is not well understood. The second approach is to use sparse systems in order to compress the public key, but this often leads to a loss in security. 

For public key encryption, we need the resulting equation system to only have one solution and so we must have an over-defined system i.e. the public key must have more polynomials than variables. Currently there are not many multivariate public-key encryption schemes that are considered secure. 

Multivariate cryptography can also be used for pseudo random-number generators, cryptographic hash functions and symmetric encryption, e.g. the symmetric block gopher QUAD.

What about Elliptic-Curve Cryptography?

I have talked about elliptic curve cryptography in previous blog posts, so why isn’t this mentioned?

Due to the novelty of these cryptographic schemes there is not great confidence in them yet. So they are not currently consensually considered as candidates for post-quantum public-key encryption. 

This is the first installation in my series about post-quantum cryptography. Anything you want me to talk about in particular? M x

Is the COVID-19 Tracing App secure?

There has been a lot of talk about the COVID-19 tracing app that has been recently released. The simple premise is that the app will use Bluetooth signals to log on when smartphone owners are close to each other, so if someone develops COVID-19 symptoms, an alert can be sent to other users they may have infected. However, countries and organisation developing the apps have opted for two different types of systems to achieve this: centralised systems or decentralised systems. First, I will what these are in general.

Centralised Systems

Centralised systems rely on a single server as a core distribution centre in the communication with end users. From a functional perspective they often imply that each entity involved in the software stream has a specific, distinct role. For example, when streaming a movie on Netflix, Netflix’s central server provides the video; the user consumes it. However, this also means that if the central server is compromised, the entire network is.

Decentralised Systems

Decentralised systems eliminate the need for a central entity and rely on multiple servers or end-user devices to cooperate and undertake a given task. Each of these entities is tasked with a similar role. These systems are not a novel concept and in fact there are a vast array of places in which it has been implemented, such as blockchain technology. Most decentralised systems that preserve privacy focus on ensuring either the confidentiality and anonymity of personal data (such as ‘TOR’) or user control over your personal data (such as the MIT project ‘Enigma’).

In context of COVID-19 Tracing Apps

Centralised contact-tracing apps store a user’s Bluetooth ID in a central database as well as the Bluetooth IDs of phones they have come into contact with (and any other data that’s being collected), enabling better visibility of data by health services or governments.

Decentralised contact-tracing apps only stop a user’s Bluetooth ID (and any other data being collected) in a central database and contact-tracing is done at the phone level, without sharing the information centrally. This allows for stronger data privacy.

Source: BBC News

There is a key trade-off between these two approaches: do we want to maximise data availability to health services or do we want to protect privacy of individuals? Furthermore, should it be up to individual governments or companies to make this choice? This is especially important as these two systems don’t interact well with each other, meaning that the fact that various countries are opting for different systems may prove disastrous for allowing tracing across borders and so quarantine rules may have to stay in place even with the introduction of the app.

UK App – Apple and Google are involved?

NHS officials initially decided to build a centralised system, but the NHS could not get the same accuracy as if it was using Apple and Google’s software. The second version of England’s app uses Apple and Google’s technology and opts for the decentralised approach.

The ecosystems of Apple and Google are fundamental to the NHS app. The app uses the Apple and Google system to conduct the Bluetooth contact tracing. This is achieved through an API and require some of the latest versions of the Android and iOS operating systems to run. The companies have favoured the method that puts people’s privacy at the forefront in order to stop the technology from being used maliciously.

What are your thoughts on the COVID-19 tracing app? M x

Elliptic Curves: The Basics

Working over the rationals (or more precisely any field with characteristic 0) an elliptic curve is a curve given the equation

such that the discriminant, which is 4A3 + 27B2, is non-zero. Equivalently, the polynomial on the right hand side has distinct roots, ensuring that the curve is non-singular. Though we restrict our attention to these non-singular curves we note that if the right hand side is a cubic polynomial, there are only two types of singular curves, corresponding to whether there is a double root (node) or triple root (cusp).

Source: Wolfram Mathworld

Point at Infinity

The point at infinity is an important point that always lies on an elliptic curve. For those who have studied algebraic geometry this is a familiar concept and comes from defining a projective closure of the equation defining the elliptic curve. However, informally it can be described as an idealised limiting point at the ‘end’ of each line.

If you imagine a vertical straight line, which intersects the elliptic curve at most two times.

The point at infinity is the point at which the two ends of this vertical line ‘meet’.

The reason that elliptic curves are amazing objects is because we can use geometry to make the points on the curve a group. Therefore we can use tools from algebraic number theory to study them.

Making Points on an Elliptic Curve into a Group

This is done using the chord and tangent process:

We denote the point at infinity on an elliptic curve E over Q as OE. E meets each line in 3 points, counted with multiplicity. Given two points on E, say P and Q, let R be the third point of intersection of PQ and E. Then P ⊕ Q is the third point of intersection of OER (vertical line through R) and E.

Source: jeremykun.com

If P = Q we take the tangent at P instead of the line PQ.

Then E with the group law on points defined above, denoted by (E, ⊕), is an abelian group:

  • The fact that is abelian is clear by construction
  • Identity: OE – this is why the point at infinity is such an important point and exists on all elliptic curves.
  • Inverses: Given a point P, let S be the point of intersection of the tangent at OE and E. Then let Q be the intersection of PS and E. Then the inverse of P is defined to be Q. Note that if OE is a point of inflection (point of multiplicity 3) then S = OE in the above.
  • Associativity: This is much harder to prove. It can be done by identifying (E, ⊕) with a subgroup of the Picard Group, which related to something called divisors.

Divisors are a tool for keeping track of poles and zeroes. For example, suppose a function g has a zero at a point P of order 3, and a pole at another point Q of order 2, and a pole at O of order 1 (note the number of zeroes and poles are equal, as they must be for a function). Then using divisors, we can say all this concisely as follows:

div g=3P−2Q−O

More precisely, we can define a divisor D to be a ‘formal sum’ of points on E (meaning that we write a sum of points using a + symbol but no actual operation is defined), say

Then the degree of a divisor is the sum of the coefficients.

This set of divisors forms a group, Div(E), generated by the points on E. Immediately we can identify a subgroup of Div(E), namely the divisors of degree zero denoted Div0(E).

We can also define an equivalence relation ~ on divisors: D1, D2 ∈ Div(E) are linearly equivalent, written D1 ~ D2, if exists an f such that div(f) = D1 – D2.

We can now introduce the Picard Group. It is a subgroup of Div(E), defined by quotienting out by this equivalence relation

A subgroup of the Picard group is given by

We’re now ready to go back to talking about elliptic curves. The point of this discussion is that we know (Pic0(E), +) is a group which has the associative property. Furthermore, we can show that we have a bijection between (E, ⊕) and (Pic0(E), +) that preserves the group structure i.e. we have an isomorphism of groups. So, using this isomorphism we can identify the two groups and deduce that (E, ⊕) is also associative.

Consequence

Say we started looking at points defined over Q (denoted by E(Q)). A natural question is to ask how we know that the addition or inverses of these points remains in Q?

We defined the group law by looking at the intersections of lines and curves. So, working through the algebra, we can get explicit equations for the addition of points and inverses. For example if we have an elliptic curve E over Q and a point P = (x,y) in E(Q), then -P = (x, -y).

These explicit equations are useful because they tell us that the points do indeed remain defined over Q. More precisely, we find that (E(Q), ⊕) is a subgroup of (E, ⊕):

  • The identity OE is in E(Q) by definition
  • (E(Q), ⊕) is closed under addition and has inverses by the explicit formulae
  • Associativity and commutativity is inherited from (E, ⊕).

Note: This in fact holds for any field K, not just Q, but we must be a bit more careful, as the elliptic curve may not be expressible in the nice form y2 = x3 + Ax + B so the formulae are a bit messier. The reason why this is important is that we often want to consider elliptic curves over finite fields, something I will explore in future posts.

M x